Solving Schrodinger Equation - Linear Algebra with LAPACK

Today I solve the Time-independent Schrodinger equation (TISE) using the finite difference method that I explained in previous blog and the Matrix method. Being able to solve the TISE numerically is important since only small idealized system can be solved analytically. I consider here only one dimensional case for a particle in a potential V(x). The one dimensional TISE is

-(1/2) [d^2 psi(x) /dx^2] + V(x) psi(x) = E psi(x)

Note I use natural unit m = hbar = 1.

The first step we need to do is to transform differential equation into matrix equation. To use finite difference, we evaluate the wavefunction, psi(x) i.e. the solution of the TISE, at N+1 grid points with spacing dx, {psi(i)}. Similarly the potential is evaluated at i*dx i.e. V(i). Note i=0, 1, ..., N. The computational length is L = N*dx.

Using central finite difference,

d^2 psi(x)/dx^2 = (psi(x+dx) - 2psi(x) + psi(x-dx))/dx^2
= ( psi(i+1) - 2psi(i) + psi(i-1) )/dx^2

This transforms the 1D TISE into
-( psi(i+1) - 2psi(i) + psi(i-1) )/(2dx^2) + V(i)psi(i) = E psi(i)

after simple manipulation, we have

-psi(i+1) + (2 + (2dx^2)V(i))psi(i) - psi(i-1) = (2dx^2)E psi(i)

For computational convenience we use the boundary conditions where psi(0)=psi(L)=0;

The above discretized 1D TISE and using boundary conditions, in matrix form, is given by





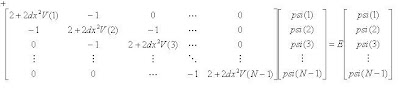
This is an eigen matrix problem. To solve it I use LAPACK function dstev_() to compute eigenvalues for symmetric matrix. As an example I consider a finite square well potential given by V(x) = 1 for |x-5|>1 and V(x) = 0 for |x-5|<1 and grid spacing dx=0.1.


--- eigen.c ---

#include <stdio.h>
#include <math.h>

#define N 100

int main(void)
{
int i;
double dx = 0.1;
double dxsq = dx*dx;
double hdiag[(N-1)],hoff[(N-2)]; //hold diagonal and off-diagonal
double v[(N-1)];
char jobType = 'V';
long int n = (N-1);
long int info,ldz = N-1;
double work[2*N-4];
double z[(N-1)][(N-1)];

/* initialize V(x) */
for(i=0;i<(N-1);i++){
if(fabs((i+1)*dx - 5)<1){ v[i]= 0;}
else v[i] = 1;
}

/* initialize hoff */
for(i=0;i<(N-2);i++){
hoff[i] = -1;
}
/* initialize hdiag */
for(i=0;i<(N-1);i++){
hdiag[i] = 2.0 + 2.0*dxsq*v[i];
}

dstev_(&jobType,&n,hdiag,hoff,z,&ldz,work,&info);

/* Print results for four eigen states */
printf("info = %ld\n",info);
printf("The Lowest Four Eigen Values \n");
for(i=0;i<4;i++){
printf("%ld %lf\n",i,hdiag[i]/(2.0*dxsq));
}

printf("The Lowest four Eigen Vectors\n");
printf("x groundstate 1st 2nd 3rd \n");
for(i=0;i<(N-1);i++){
printf("%lf %lf %lf %lf %lf\n",i*dx,z[0][i],z[1][i],z[2][i],z[3][i]);
}

return 0;
}



To compile:

gcc eigen.c -lm -llapack -o try

Discrete Fourier Transform using FFTW

If we have a time series data and we want to know the frequency content of it, then we need to perform Fourier transformation. This can be done numerically using available mathematical softwares such as Matlab, Mathematica and Maple. For C programming language, I mostly use FFTW since it is free and easy to use on linux OS and in Cygwin on Windows.

To understand how to do DFT, let us a look at Fourier transform of a square function given by f(t) = 1 for |t-2|<=1 and f(t) = 0 for |t-2|>1. We consider the function at interval (0,4). First discretize the data into grids with spacing 0.1.

--- try_fftw.c ---

#include <stdio.h>
#include <math.h>
#include <fftw3.h>

#define N 40

int main(void)
{
int i;
double dt, t;
fftw_complex *f, *g;
fftw_plan p;

dt = 0.1;
/* allocate memory for f and g */
f = (fftw_complex*) fftw_malloc(sizeof(fftw_complex) * N);
g = (fftw_complex*) fftw_malloc(sizeof(fftw_complex) * N);

/* compute square function f(x) */
for(i=0;i<N;i++){
t = i*dt;
if(fabs(t-2)<=1){
f[i][0] = 1;
f[i][1] = 0;
}
else{
f[i][0] = 0;
f[i][1] = 0;
}
}

/* Print f(t) */
printf(" -- i f(t) -- \n");
for(i=0;i<N;i++){
printf("%d %e \n", i, f[i][0]);
}

/* create plan */
p = fftw_plan_dft_1d(N, f, g, FFTW_FORWARD, FFTW_ESTIMATE);

/* perform FFT */
fftw_execute(p);

/* Print results */
printf(" -- i g(w) -- \n");
for(i=0;i<N;i++){
printf("%d %e %e \n", i, g[i][0], g[i][1]);
}

/* Free memory */
fftw_destroy_plan(p);
fftw_free(f);
fftw_free(g);

return 0;
}


-------

To compile use:

 gcc try_fftw.c  -lm -lfftw3 -o try  

Results are shown in the figures below





Ref: FFTW3 manual

Numerical Differentiation Formulas

In Physics, to simulate physical system, we usually encounter ordinary or partial differential equations. Let us consider a function or a field f(x) which satisfies a specified differential equation. To solve the differential equation, we first approximate the function f(x). The approximation can be in a form of Fourier series, a polynomial and a discrete functions. Today I will only consider the discrete function. The function f(x) is approximated in an interval (a,b) by (N+1) discrete values given by {f(i)} where f(x) = f(i*h) , h = (b-a)/N, i=0,1,2 ... N. Then we need to approximate derivatives in the differential equation.

The numerical differentiations that I often used are central finite difference schemes:

1) d f(x)/dx = [f(x+h)-f(x-h)]/2h + O(h^2)
= [f(i+1)-f(i-1)]/2h (second order accurate)

2) d^2 f(x)/dx^2 = [f(x+h)-2f(x) + f(x-h)]/h^2 + O(h^2)
= [f(i+1)-2f(i)+f(i-1)]/h^2 (second order accurate)

d^2 f(x)/dx^2 = [-f(x+2h)+16f(x+h)-30f(x) + 16f(x-h)-f(x-2h)]/(12h^2) + O(h^4)
= [-f(i+2)+16f(i+1)-30f(i)+16f(i-1)-f(i-2)]/(12h^2)
(fourth order accurate)

3) d^3 f(x)/dx^3 = [f(x+2h)-2f(x+h) +2 f(x-h)-f(x-2h)]/(2h^3) + O(h^2)
= [f(i+2)-2f(i+1)+2f(i-1)-f(i-2)]/(2h^3) (second order accurate)

As an example, Let us compute derivatives for trigonometric function sin(Pi x) in the interval (0,1). In C programming language, can be written as

--- num_diff.c ---

/* Numerical Differentiation
* by I Wayan Sudiarta Oct 2007
*/

#include<math.h>
#include<stdio.h>

#define N 20
#define PI 3.141592653589793

int main(void)
{
int i;
double h, hsq, hcb;
double f[N+1], f1[N+1], f2[N+1], f2b[N+1], f3[N+1];

h = 1.0/((double)(N));

hsq = h*h;
hcb = h*hsq;

/* Compute f[i] */
for(i=0;i<=N;i++){
f[i] = sin(i*PI*h);
}

/* Compute derivatives */
for(i=2;i<(N-1);i++){
f1[i] = (f[i+1]-f[i-1])/(2*h);
f2[i] = (f[i+1]-2*f[i]+f[i-1])/(hsq);
f2b[i]= (-f[i+2]+16*f[i+1]-30*f[i]+16*f[i-1]-f[i-2])/(12*hsq);
f3[i] = (f[i+2]-2*f[i+1]+2*f[i-1]-f[i-2])/(2*hcb);
}


/* Print results */
printf("x f1(x) f2(x) f2b(x) f3(x) \n");
for(i=2;i<(N-1);i++){
printf("%e %e %e %e %e \n", i*h, f1[i], f2[i], f2b[i], f3[i]);
}
return 0;
}

Ref: CRC Standard Mathematical Tables, 27th Edition, 1974

Welcome....The beginning

Welcome... to my physics simulation blog

The purpose of this blog is to collect all things that I found interesting which are related to physics simulations. I do physics simulations almost everyday. While working, reading books and searching the internet I often discover new interesting stuff for physics simulations. One might say that this blog is a tutorial of physics simulation.

Currently I am doing simulation of few electrons system at thermal equilibrium. Interesting stuff!

I hope this blog can be useful for people like me who are learning and working using simulations.